可以从圆周率里找到所有人的生日、银行卡密码和手机号码吗？

一般人大概是在小学四五年级就会接触到计算圆面积的相关课程，而我们知道要计算圆的面积，就需要用到圆周率。那什么是圆周率呢？

圆周率的具体定义是圆的周长和它的直径的比值，我们常用希腊字母π来表示圆周率。

这看似简单的圆周率，实际上却是一个极其让学者们头疼的常数。首先，它是一个无理数，无限不循环。因此，我们没有办法完全用分数来表示圆周率。

但是“圆”是我们日常生活中经常使用的图形，因此把圆周率进一步精确成为实际用途中十分必要的工作。而各大文明古国也纷纷在这方面有一些突破。

精确“圆周率”

中国作为四大古国之一，在计算圆周方面当然是有巨大成就的。比较有代表性的是南北朝时期的数学家祖冲之，他就把圆周率精确到了小数点后7位，也就是在3.1415926~3.1415927的区间内。

而在西方，其实也有一位计算圆周率的大神，这个人叫做阿基米德。阿基米德发第一个使用穷竭法来计算圆周率。

具体来说，就是用一个给圆做外切和内接正多边形，这样就可以得到圆的一个面积范围。当用边数更多的外切和内接多边形时，就可以得到一个更为精确的面积范围。

阿基米德做到了正96边形，把圆周率的范围缩小到了3.1408~3.1429的区间内。后来有人用这个办法精确到了小数点后39位。而物理学界的大神牛顿也曾利用无穷级数法，把圆周率精确到了小数点后15位。

但这些显然是不够的，科学家在计算圆周率的这条路上渐行渐远。随着计算机的出现，计算圆周率这件事上被大规模地推荐。在2015年之前，已经可以计算到小数点后10^13位。而目前的已经计算到了2*10^14位。不过这样去计算的主要目的已经不是为了科研的目的，而主要是测算计算机元件的性能。客观地说，无论计算机如何计算，其实意义并不大了，毕竟按照无理数的定义来看，计算圆周率这件事是没有个头的。

不过，一直以来都流传这样的一种说法，那就是在圆周率的小数当中可以找到所有的人的生日、银河卡卡密，甚至是手机号。实际上，它包含的不仅仅这些，而是远比这些还要多。不信，我们就来算算看。

圆周率包含所有的银行卡卡密吗？

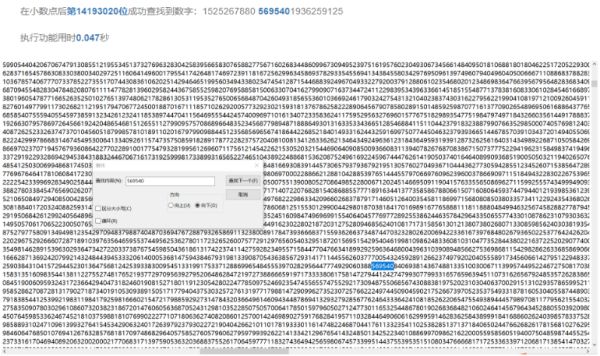
银行卡卡密是六位数的，因此，这个问题的本质其实就是在圆周率的小说当中是不是包含所有的六位数，也就是从000000到999999。我们当然不可能一点点去找，不过我们可以利用计算机程序来找，这个事其实很简单，有很多人都试过了。要找全所有的六位数，只需要数到小数点后的14,118,307就够了，最后出现的六位数是569540。

稍微懂得数学的童鞋，其实还可以利用数学方法求解，我们得到这样的结果：

在圆周率小数点前100万位中找到密码的概率大概是60%；

在圆周率小数点前230万位中找到密码的概率大概是90%；

当然，我们就可以利用同样的办法来找所有的生日。生日是八位数的，但是这个问题并不是找到所有的八位数，而只是一部分的八位数。我们都知道，目前被官方所承认的，并且记录在案证据的，还活着的，最长寿的人没有超过120岁的。因此，所有人的生日范围也就是从1900/01/01到2020/02/08之间。通过刚才提到的方法，我们会发现圆周率小数点后10亿位以内就可以把所有的生日都找全。

同样是用数学的办法，我们可以得到：在圆周率小数点前3.51亿位中找到所有人生日的概率大概是50%。

最后，我们来看看圆周率的小数点是不是包含所有的手机号。手机号是11位数的，不过，手机号的第一位数是1是固定的，因此，就是从10000000000到19999999999之间。当然，实际上手机号并没有这么宽的范围，这里只是为了方便做了些许简化。如果这个区间要用计算机来跑的话，一般的计算机应该跑不出结果的，并不是说圆周率的小数点不含所有的手机号，而是因为计算量实在太大了，一般的计算机做不到。编程的方式不好弄，我们可以同样利用数学的办法来实现，通过数学推断，我们可得到，要把手机号找全至少需要计算到圆周率小数点后4606亿位。

所以，接下来的问题就是，圆周率的小数点是不是可以持续到小数点4606亿位之后。首先，圆周率是无理数，因此，从理论上来说是肯定存在，这个其实不需要证明了。其次，如今科学家利用计算机已经把圆周率的小数点推进到了224591亿位，这要比这个要求大了两个数量级。因此，绝对是可以找得到所有的手机号的。

所以，无论是卡密，生日，还是手机号其实都可以在圆周率小数点后找到。